점곱은
벡터로 스칼라를 계산하는 이항연산입니다. 점곱 자체가 스칼라이기 때문에 점곱을 ‘스칼라곱(scalar product)’이라고도 하고, 스칼라곱을 사용하는 모든 유클리드 공간은 내적(inner product)공간이므로, 스칼라곱을 ‘유클리드 내적’ 또는
단순히 ‘내적’ 이라 부르기도 합니다.
점곱은
벡터공간에서 정의된 이중 선형을 사용합니다. 두 개의 벡터 A와 B가 있을 때 B를 A와 동일한 방향의 성분으로 변환하여 구한 스칼라 값을
A의 스칼라 값에 곱하여 구합니다. 따라서 A,
B를 2차원 또는 3차원
공간의 벡터, θ
를 이들이 이루는 각이라
할 때 A,
B의 점곱을
로 정의합니다. 점곱은 교환법칙이 성립하며, 분배법칙도 성립합니다.
그리고 |B|cosθ 는 A에 투영한 B이므로
라 해석할 수 있습니다. 혹은 교환법칙이 성립하므로 반대로
로 쓸
수도 있습니다.
단위벡터에
점곱을 적용해 봅시다. 3차원 벡터의 단위벡터들을 서로 점곱하면 같은 성분의 단위벡터끼리는 평행하여
두 단위벡터가 이루는 각 θ
는 0이고, 다른 성분의 단위벡터끼리는 수직이므로 두 단위벡터가 이루는
각 θ
는 π/2입니다. 따라서
다음과 같습니다.
i,
j, k는 x,
y, z 축에 나란한 단위벡터 입니다.
두 벡터의
내적을 벡터의 성분으로 표현하는것도 가능합니다. 두 개의 벡터
를 성분으로
쓰면
이고, 분배법칙을 이용하여 단위벡터를 정리하면
이 됩니다. 따라서
은 두
벡터 A와 B의 점곱을 직각좌표 성분으로 나타내었다 합니다. 이 과정에서 점곱은 같은 성분끼리 곱한 뒤 모두 더한다는 규칙을 얻을 수 있습니다. 이 규칙을
이용하여 벡터 A와 A를 점곱해 보면
이므로
다음과 같습니다.
이것은
피타고라스 정리를 삼차원으로 확장한 것으로 볼 수 있습니다. 또한 A의 스칼라 값은 ‖A‖와 같습니다. ‖A‖는 A의 노름(norm)이라
합니다. 따라서 점곱을
위 식을
응용하여 두 벡터가 이루는 각 θ 를 구할 수 있습니다.
방법은 다음과 같습니다.
이제 정의들을
정리해 봅시다.

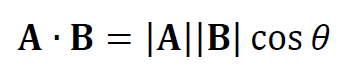









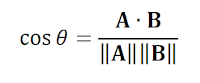

Sportsbet Betting on Virtual Reality - Legalbet.co.kr 10bet 10bet ラッキーニッキー ラッキーニッキー m88 m88 온카지노 온카지노 메리트카지노 메리트카지노 카지노사이트 카지노사이트 1xbet korean 1xbet korean sbobet ทางเข้า sbobet ทางเข้า 227 bet365 Archives - Legalbet.co.kr - KRK - Sports
답글삭제