점곱(dot product, 내적) : http://ujerspace.blogspot.kr/2015/09/dot-product.html
을 참고 하시면 더욱 이해가
빠릅니다.
‘벡터곱(cross
product)’은 다음과 같은 형태로 씁니다.
두 벡터를
점곱(내적)했을 때 방향이 없는 스칼라가 구해지지만, 두 벡터를 벡터곱하면 두 벡터 수직한 방향의 벡터를 구할 수 있습니다. 두
벡터의 수직한 방향의 벡터는 3차원 공간에서 예를 들면 x 축의 벡터와 y 축의 벡터 모두에 수직하는 z 축의 벡터와 같은 것을 말합니다. 벡터곱의 정의는 기하학적으로 다가가 평행사변형으로부터 얻을 수 있습니다. 평행사변형의
넓이는 밑변과 높이의 곱으로 구해집니다.
그림에서 평행사변형의 밑변은 ‖A‖, 높이는 ‖B‖ sin θ 는 A와
B가 만드는 높이라는
것을 알 수 있습니다. ‖A‖은
벡터 A의 노름(norm)입니다. 따라서 평행사변형의 넓이 S는
입니다. S는 방향이 없는 스칼라입니다. S에
A와 B를 품는 평행사변형
평면에 수직이고, 길이가 1인 단위벡터(unit vector) n hat을 연산해줍니다.
이 결과가 벡터
A와 B를 벡터곱한
결과와 같습니다. 따라서 A와 B의 벡터곱을
으로 정의합니다. 여기서 오른손 A×B가 A와 B에 항상 직교(수직)함을 확인하고 싶다면 점곱(내적)을
이용하면 됩니다. 서로 수직인 두 벡터를 점곱(내적)한 결과는 0입니다.
여기서는 오른손 좌표계를 적용하여 오른손법칙(right-hand rule)을
사용합니다. 즉, A에서
B로 향해 오른손을 꽉 쥐었을 때, 그
엄지손가락 방향이 n hat과 A×B의 방향입니다.
벡터곱은 분배법칙이 성립합니다.
그리고 오른손법칙에 의해 교환법칙은 성립하지 않지만 반교환법칙은 성립합니다.
결합법칙은 성립하지 않습니다.
이제 x,
y, z축에 나란한 단위벡터 i, j, k끼리 벡터곱을 해봅시다. 평행하는 같은 단위벡터끼리 벡터곱을 하면
이 결과가 나옵니다. 즉, 평행한 두 벡터를 벡터곱하면
0을 얻습니다.
수직하는 다른 단위벡터끼리 벡터곱을 하면
즉,
이고, 반교환법칙이 성립하므로
이러한 결과를 얻을 수 있습니다.
A 성분과 B 성분의 벡터곱을 분배법칙 해봅시다.
이 복잡한 식은
행렬식을 사용해 간단하게 정리할 수 있습니다.
마지막으로 응용하여 라그랑주의 항등식을 유도해봅시다. 벡터곱의 크기는
A×B에 노름(norm)과
같으므로
입니다. 양변을 제곱합니다.
sin^2(θ )+cos^2(θ )=1이므로 sin^2(θ )=1- cos^2(θ )을 대입합니다.
점곱(내적)의 정의에
의해 다음과 같습니다.
따라서 라그랑주의 항등식
을 얻을 수 있습니다.
이제 정의들을
정리해 봅시다.






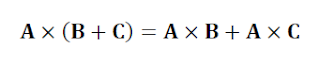














댓글 없음:
댓글 쓰기