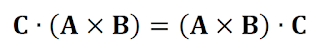스칼라 삼중곱(scalar triple product)

‘스칼라 삼중곱(scalar triple product)’의 형태는 다음과 같습니다.

두 벡터의 벡터곱(cross product)을 나머지 벡터와 스칼라곱(scalar product)한 것으로 정의합니다. 스칼라 삼중곱의 정의는 기하학적으로 평행육면체의 부피로부터 얻을 수 있습니다. 평행육면체의 부피는 밑변의 넓이와 높이의 곱으로 구해집니다.

[그림 1]의 평행육면체의 밑면의 넓이는 ‖B×C‖입니다. ‖B×C‖는 변이 ‖B‖, ‖C‖이고, 각도가 θ 인 평행사변형의 넓이이기 때문입니다. 또한, 평행육면체의 높이는 ‖A‖cosΦ 입니다. 그러면 평행육면체의 부피 V 는

이므로, 스칼라 삼중곱의 절댓값은 3개의 벡터로 만들어지는 평행육면체의 부피와 같다는 것을 알 수 있습니다. 하지만 스칼라 삼중곱의 절댓값 |A∙(B×C)|는 일반적으로 쓰이는 부피이고, A와 (B×C)가 이루는 각 Φ 가 예각이냐 또는 둔각이냐에 따라서 양의 부피이거나 또는 음의 부피가 됩니다. 그러므로

라 할 수 있습니다.

이제 스칼라 삼중곱을 단위벡터(unit vector)를 이용하여 행렬식(determinant)으로 전개해봅시다.

이므로 일반적으로 스칼라 삼중곱은 다음 공식

로부터 계산합니다. 여기서 3×3 행렬식은 두 행을 두 번 교환해도 같으므로(기본행연산) 첫 번째 성질을 알 수 있습니다.

위 스칼라 삼중곱에 절댓값을 씌우면 양의 부피와 같습니다. 이와 같이 음의 부피로부터 두 번째 성질 또한 알 수 있습니다.

또한,

위 식에서 점곱(dot product)은 교환법칙이 성립하므로

따라서 세 번째 성질은 다음과 같습니다.

즉, 스칼라 삼중곱에서는 점(dot, ∙ )과 가위(cross, × )를 맞바꿀 수 있습니다.

이제 정의들을 정리해 봅시다.

정의 1 평행육면체의 부피 V

정의 2 스칼라 삼중곱의 직각좌표 성분(행렬식)

정의 3 스칼라 삼중곱의 성질

같이 참고하면 좋은 글

점곱(dot product, 스칼라곱, 내적): http://ujerspace.blogspot.kr/2015/09/dot-product.html

벡터곱 (cross product, 가위곱): http://ujerspace.blogspot.kr/2015/09/cross-product.html

벡터곱(cross product)

이 글을 읽기전 점곱(dot product, 내적)에 대해 배운적이 없다면

점곱(dot product, 내적) : http://ujerspace.blogspot.kr/2015/09/dot-product.html

을 참고 하시면 더욱 이해가 빠릅니다.​

​

‘벡터곱(cross product)’은 다음과 같은 형태로 씁니다.

두 벡터를 점곱(내적)했을 때 방향이 없는 스칼라가 구해지지만, 두 벡터를 벡터곱하면 두 벡터 수직한 방향의 벡터를 구할 수 있습니다. 두 벡터의 수직한 방향의 벡터는 3차원 공간에서 예를 들면 x 축의 벡터와 y 축의 벡터 모두에 수직하는 z 축의 벡터와 같은 것을 말합니다. 벡터곱의 정의는 기하학적으로 다가가 평행사변형으로부터 얻을 수 있습니다. 평행사변형의 넓이는 밑변과 높이의 곱으로 구해집니다.

그림에서 평행사변형의 밑변은 ‖A‖, 높이는 ‖B‖ sin θ 는 A와 B가 만드는 높이라는 것을 알 수 있습니다. ‖A‖은 벡터 A의 노름(norm)입니다. 따라서 평행사변형의 넓이 S는

입니다. S는 방향이 없는 스칼라입니다. S에 A와 B를 품는 평행사변형 평면에 수직이고, 길이가 1인 단위벡터(unit vector) n hat을 연산해줍니다.

이 결과가 벡터 A와 B를 벡터곱한 결과와 같습니다. 따라서 A와 B의 벡터곱을

으로 정의합니다. 여기서 오른손 A×B가 A와 B에 항상 직교(수직)함을 확인하고 싶다면 점곱(내적)을 이용하면 됩니다. 서로 수직인 두 벡터를 점곱(내적)한 결과는 0입니다.

여기서는 오른손 좌표계를 적용하여 오른손법칙(right-hand rule)을 사용합니다. 즉, A에서 B로 향해 오른손을 꽉 쥐었을 때, 그 엄지손가락 방향이 n hat과 A×B의 방향입니다.

벡터곱은 분배법칙이 성립합니다.

그리고 오른손법칙에 의해 교환법칙은 성립하지 않지만 반교환법칙은 성립합니다.

결합법칙은 성립하지 않습니다.

이제 x, y, z축에 나란한 단위벡터 i, j, k끼리 벡터곱을 해봅시다. 평행하는 같은 단위벡터끼리 벡터곱을 하면

이 결과가 나옵니다. 즉, 평행한 두 벡터를 벡터곱하면 0을 얻습니다.

수직하는 다른 단위벡터끼리 벡터곱을 하면

즉,

이고, 반교환법칙이 성립하므로

이러한 결과를 얻을 수 있습니다.

A 성분과 B 성분의 벡터곱을 분배법칙 해봅시다.

이 복잡한 식은 행렬식을 사용해 간단하게 정리할 수 있습니다.

마지막으로 응용하여 라그랑주의 항등식을 유도해봅시다. 벡터곱의 크기는 A×B에 노름(norm)과 같으므로

입니다. 양변을 제곱합니다.

sin^2(θ )+cos^2(θ )=1이므로 sin^2(θ )=1- cos^2(θ )을 대입합니다.

점곱(내적)의 정의에 의해 다음과 같습니다.

따라서 라그랑주의 항등식

을 얻을 수 있습니다.

이제 정의들을 정리해 봅시다.

점곱(dot product)

‘점곱(dot product)’은 다음과 같은 형태로 씁니다.

점곱은 벡터로 스칼라를 계산하는 이항연산입니다. 점곱 자체가 스칼라이기 때문에 점곱을 ‘스칼라곱(scalar product)’이라고도 하고, 스칼라곱을 사용하는 모든 유클리드 공간은 내적(inner product)공간이므로, 스칼라곱을 ‘유클리드 내적’ 또는 단순히 ‘내적’ 이라 부르기도 합니다.

점곱은 벡터공간에서 정의된 이중 선형을 사용합니다. 두 개의 벡터 A와 B가 있을 때 B를 A와 동일한 방향의 성분으로 변환하여 구한 스칼라 값을 A의 스칼라 값에 곱하여 구합니다. 따라서 A, B를 2차원 또는 3차원 공간의 벡터, θ 를 이들이 이루는 각이라 할 때 A, B의 점곱을

로 정의합니다. 점곱은 교환법칙이 성립하며, 분배법칙도 성립합니다.

그리고 |B|cosθ 는 A에 투영한 B이므로

라 해석할 수 있습니다. 혹은 교환법칙이 성립하므로 반대로

로 쓸 수도 있습니다.

단위벡터에 점곱을 적용해 봅시다. 3차원 벡터의 단위벡터들을 서로 점곱하면 같은 성분의 단위벡터끼리는 평행하여 두 단위벡터가 이루는 각 θ 는 0이고, 다른 성분의 단위벡터끼리는 수직이므로 두 단위벡터가 이루는 각 θ 는 π/2입니다. 따라서 다음과 같습니다.

i, j, k는 x, y, z 축에 나란한 단위벡터 입니다.

두 벡터의 내적을 벡터의 성분으로 표현하는것도 가능합니다. 두 개의 벡터

를 성분으로 쓰면

이고, 분배법칙을 이용하여 단위벡터를 정리하면

이 됩니다. 따라서

은 두 벡터 A와 B의 점곱을 직각좌표 성분으로 나타내었다 합니다. 이 과정에서 점곱은 같은 성분끼리 곱한 뒤 모두 더한다는 규칙을 얻을 수 있습니다. 이 규칙을 이용하여 벡터 A와 A를 점곱해 보면

이므로 다음과 같습니다.

이것은 피타고라스 정리를 삼차원으로 확장한 것으로 볼 수 있습니다. 또한 A의 스칼라 값은 ‖A‖와 같습니다. ‖A‖는 A의 노름(norm)이라 합니다. 따라서 점곱을

위 식을 응용하여 두 벡터가 이루는 각 θ 를 구할 수 있습니다. 방법은 다음과 같습니다.

이제 정의들을 정리해 봅시다.