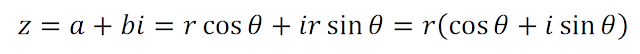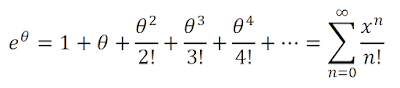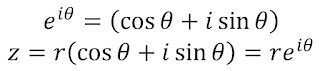복소수의 사칙연산

이 글을 읽기 전 복소수에 대한 기초지식이 없다면

제목: 복소수
http://ujerspace.blogspot.kr/2015/10/complex-number.html

위 글을 읽고 참고하시면 더욱 좋습니다.


           복소수는 0으로 나누는 경우를 제외하면 사칙연산을 자유롭게
행할 수 있습니다. 복소수를 더하고 빼거나, 곱할 때, 복소수는 대응 벡터연산과 같이 일반적인 연산규칙을 따릅니다.

▶ 복소수의 덧셈과 뺄셈, 곱셈

           두 복소수가 같다고 할 때에는, 두 복소수의 실수부와 허수부가
모두 같다고 함을 의미합니다. 예를 들어 임의의 복소수는 직교형태인 x +iy 의 형태로 쓸 수 있는데 두 복소수

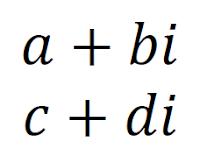식 (1.1)

가 있고,

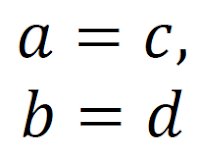식 (1.2)

라고 하면, 두 복소수 a +ib 와 c +id 는 같은 복소수라 합니다.

위와 같으므로, 복소수의 덧셈은 실수부와 허수부끼리 더함으로써 연산이 이루어 집니다.

식 (1.3)

복소수의 뺄셈과 복소수와 실수와의 곱셈 또한 같습니다.

식 (1.4)

식 (1.5)

복소수끼리 곱할 때 에는 일반적인 연산규칙을 따르고,

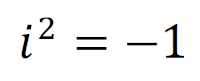식 (1.6)

와 같이 취해 주는 것만 기억해주면 됩니다. 예를 들어 다음과 같습니다.

식 (1.7)

그러므로 복소수끼리의 곱셈은 다음 정의를 암시합니다.

식 (1.8)

▶ 켤레 복소수

           임의의 복소수

식 (1.9)

가 있을 때 복소수 z 의 켤레(coujugate)복소수는 z̅ (“z 바”라 읽음) 혹은 z^* 로 표시되고, 정의는 다음과 같습니다.

식 (1.10)

[그림 1]에서 볼 수 있듯이 기하학적으로 z̅ 는 z 를 실수축에 대해 반사시킨 상입니다.

[그림 1] 복소수의 켤레

즉, z̅ 는 z 의 허수부의 부호를 반대로 함으로써 얻어집니다.

예를 들어 복소수 z 가

식 (1.11)

라고 하면, z 의 켤레 복소수는

식 (1.12)

이와 같습니다.
또한, 두 복소수의 합에 대한 켤레는 이 수의 켤레들의 합과 같습니다,

식 (1.13)

여기서 주의해야 할 점은 만일 복소수 z 가

식 (1.14)

이고, f 와 g 가 복소수라면 z 의 켤레 복소수는

식 (1.15)

이가 됩니다.

▶ 모듈러스(modulus)

           복소수 z 를 R^2 의 벡터로 생각하는 겨우 벡터의 길이 또는 노름을 z 의 모듈러스(또는 절대값)라고 합니다.

임의의 복소수

식 (1.16)

가 있을 때,

식 (1.17)

이고, 극좌표계에서는

식 (1.18)

이고,

식 (1.19)

이므로 즉,

식 (1.20)

가 됩니다. 여기서 a, b, r 은 실수이기 때문에 zz̅ 는 항상 실수이고

식 (1.21)

입니다. 따라서 z 의 모듈러스(또는 절대값)을 다음으로 정의합니다.

식 (1.22)

위의 정의에서

식 (1.23)

이면

식 (1.24)

는 실수이고,

식 (1.25)

이므로, z 의 모듈러스는 그 절대값에 지나지 않습니다. 그 이유로 z 의 모듈러스를 또한 z 의 절대값이라고 합니다.

▶ 복소수의 나눗셈

           복소수의 나눗셈을 곱셈의 역으로 정의하겠습니다. 세 복소수

식 (1.26)

가 있고,

식 (1.27)

라 할 때에 식 (1.27)은

식 (1.28)

이와 같이 표기할 수 있습니다. 식 (1.27)에서 실수부와 허수부를 같도록 놓으면

식 (1.29)

즉,

식 (1.30)

복소수 z_2 는

식 (1.31)

이므로 a_2 와 b_2 모두 영이 아님이 성립합니다. 따라서,

식 (1.32)

이고, 크라메르 공식에 의하여 식 (1.30)는 다음의 유일한 해를 갖습니다.

식 (1.33)

그러므로,

식 (1.34)

따라서, z_2≠0 에 대해서 다음과 같이 정의합니다.

식 (1.35)

식 (1.35)의 정의에 의하여 복소수를 복소수로 나눌 때에는 먼저 이 나눗셈을 분수로 표현한 후, 분자와 분모에 분모의 켤레를 곱하여 분수를 직교형태로 만듭니다. 이 방법을 쓰면 분모는 실수가 됩니다.

예를 들어 다음과 같습니다.

식 (1.36)

정리

정리 1 복소수의 덧셈

정리 1

정리 2 복소수의 뺄셈

정리 2

정리 3 복소수의 곱셈

정리 3

정리 4 복소수의 나눗셈

정리 4

정리 5 복소수의 모듈러스(절댓값)

정리 5

복소수(complex number)

▶ 복소수의 형태(꼴)

‘복소수(complex number)’란 ‘실수(real number)’와 ‘허수(imaginary number)’가 결합한 수들의 집합에 속하는 수(체의 원소)를 말합니다. 일반적으로 복소수의 집합(체)을 볼드체 C 기호로 표기하고, 편리성을 위해 단일문자 z 로 사용합니다. 복소수 z 는 ‘직교형식’으로 표현하면 다음과 같습니다.

또한, 실수의 순서쌍

으로 표기하기도 합니다. a 와 b 는 실수입니다. 여기서 a 를 z 의 ‘실수부’, b 를 z 의 ‘허수부’라고 하며, 실수부는 순서쌍 (a, b)의 첫 번째 성분을, 허수부는 순서쌍 (a, b)의 두 번째 성분을 말합니다. 그리고 i 는 -1에 제곱근을 씌운 허수단위로 즉,

▶ 허수의 역사

i 는 “가상의”를 뜻하는 imaginary의 첫 자에서 따온 것처럼 역사적으로 17세기 전까지 복소수는 “수(number)”로서 인정받지 못했습니다.

허수가 정의되기 전 1세기에 고대 그리스의 발명가이자 수학자 “헤론(Ήρων)”이 음수의 제곱근에 대한 개념을 기록하면서 허수의 개념이 최초로 나타났고, 16세기에 와서야 허수가 정의되기 시작하였습니다.

[그림 1] 헤론

1572년에는 이탈리아의 수학자 “라파엘 봄벨리(Rafael Bombelli)”가 어떠한 2차방정식에선 음수의 제곱근을 취해야만 근을 구할 수 있었기 때문에 수를 확장하여 허수라는 새로운 종류의 수를 도입하였습니다.

[그림 2] 라파엘 봄벨리

예로 다음과 같이 2차방정식이 있을 때,

위 방정식은 2차방정식의 근의 공식을 이용하여 일반해를 구할 수 있습니다.

판별식 d 가 음수일 때

여기서 허수의 개념을 도입하지 않으면 음수가 아닌 수에 대해서만 실수의 제곱근이 있으므로 식 z 는 아무 의미도 없는 식이 됩니다. 즉, 식 z 는 허수가 정의되어야만 쓸 수 있는 식이 됩니다.

이와 비슷하게 이탈리아의 수학자 “니콜로 타르탈리아(Niccolo Tartaglia)”, 이탈리아의 의사이자 수학자 “지롤라모 카르다노(Girolamo Cardano)”와 같은 수학자들도 3차와, 4차, 다항방정식의 근에 대한 공식을 발견하면서 허수의 개념을 도입하였습니다.

[그림 3] 니콜로 타르탈리아

[그림 4] 지롤라모 카르다노

17세기에 “르네 데카르트(René Descartes)”가 “가상의 수”라는 뜻으로 허수라는 용어를 사용하기 시작했고,

[그림 5] 르네 데카르트

18세기에 스위스의 수학자 “레온하르트 오일러(Leonhard Euler)”는 허수단위의 기호로 i 를 도입했습니다(전자공학과 같은 분야에서는 전류를 i 로 표기하기 때문에 허수단위를 j 로 표기하는 경우도 있습니다).

[그림 6] 레온하르트 오일러

1799년엔 노르웨이의 수학자 “카스파르 베셀(Caspar Wessel)”이 “복소평면” 모델을 정의함으로서 복소수를 기하적인 표현으로 나타내었고, 19세기에 프랑스의 수학자 “아르강(Jean-Robert Argand)”이 베셀의 논문을 프랑스어로 번역하면서 부터 복소수는 수로 인정받기 시작했습니다. 그렇기에 복소평면을 “Argand 그림”이라고도 부르기도 합니다.

▶ 복소평면

복소평면은 간단히 복소수를 기하학적으로 표현하기 위해 개발된 모델입니다. 복소평면의 형태는 데카르트 좌표계와 같습니다. xy 좌표계에서 x 축을 실수축, y 축을 허수축이라 하고, 직교형식의 복소수

는 복소평면에서 다음과 같이 표현 됩니다.

[그림 7] 직교좌표의 복소평면

Re z 는 z 의 실수부 a 를, Im z 는 z 의 허수부 b 를 표현한 것 입니다. [그림 7]은 순서쌍 (a, b)의 직교형식을 직교좌표위의 한점으로 나타낸 것 인데, 해석기하학에서는 직교좌표(x, y)대신 극좌표(r, θ )를 이용하기도 합니다. 두 좌표형태를 다음과 같이 대응할 수 있습니다.

위 식들을 직교형식에 대입하면

이와 같이 극형식으로 유도할 수 있습니다. 극형식의 복소수는 복소평면에서 다음과 같이 표현 됩니다.

[그림 8] 극좌표의 복소평면

▶ 오일러의 공식(복소지수함수)

1748년에 오일러는 복소수 지수를 정의하는데 위대한 업적을 남겼습니다.

위 식이 오일러(Euler)의 공식인데, 양변의 무한급수의 극한값이 같음을 증명하면서 발표되었습니다. 오일러의 공식을 테일러 급수를 이용하여 증명할 수 있는데, cos θ 의 급수는

이와 같고, sin θ 의 급수는

이와 같고, e^θ 의 급수는

이와 같을 때 e^iθ 의 급수를 다음과 같이 정리하여 증명할 수 있습니다.

또한, 미분을 이용하여 증명할 수도 있습니다.

라고 할 때,

이므로, 따라서

가 됩니다(단 C 는 상수). 식 (1.15)에 θ =0을 대입하면,

이 되므로

이가 됩니다. 확장하여 오일러의 공식을 ‘cis 함수’ 또는 ‘복소지수함수’를 도입하여 다음과 같이 정의합니다.

또한, 오일러의 공식을 이용하여 복소수 z 의 극형식을 다음과 같이 쓸 수 있습니다.

▶ 드 무아브르의 공식

복소수와 삼각함수의 관계에 있어 오일러 보다 먼저 업적을 보인 수학자가 있습니다. 프랑스의 수학자 ‘드 무아브르(Abraham de Moivre)’는 ‘드 무아브르의 공식’을 증명하였는데, 공식은 다음과 같습니다.

오일러의 공식을 이용하면 드 무아브르의 공식을 간단하게 유도할 수 있습니다(오일러의 공식보다 더 먼저 증명되었지만…). 유도는 다음과 같습니다.

드 무아브루의 공식을 이용하여 복소수 z 의 극형식을

이와 같이 쓸 수도 있습니다.

[그림 9] 드 무아브르

지금까지 읽은것들을 정리해봅시다.

정리 01

복소수 실수와 허수가 결합한 수들의 집합에 속하는 수

정리 02

허수단위 i

정리 03

복소수의 직교형식

정리 04

복소수의 극형식

정리 05

오일러의 공식

정리 06

드 무아브르의 공식