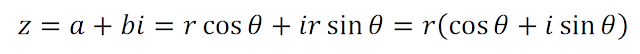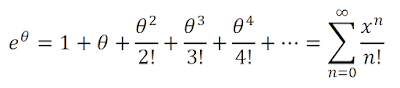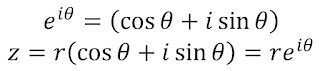하마학교[HI-KAM]: 10월 2015

▶ 복소수의 형태(꼴)

‘복소수(complex number)’란 ‘실수(real number)’와 ‘허수(imaginary number)’가 결합한 수들의 집합에 속하는 수(체의 원소)를 말합니다. 일반적으로 복소수의 집합(체)을 볼드체 C 기호로 표기하고, 편리성을 위해 단일문자 z 로 사용합니다. 복소수 z 는 ‘직교형식’으로 표현하면 다음과 같습니다.

또한, 실수의 순서쌍

으로 표기하기도 합니다. a 와 b 는 실수입니다. 여기서 a 를 z 의 ‘실수부’, b 를 z 의 ‘허수부’라고 하며, 실수부는 순서쌍 (a, b)의 첫 번째 성분을, 허수부는 순서쌍 (a, b)의 두 번째 성분을 말합니다. 그리고 i 는 -1에 제곱근을 씌운 허수단위로 즉,

▶ 허수의 역사

i 는 “가상의”를 뜻하는 imaginary의 첫 자에서 따온 것처럼 역사적으로 17세기 전까지 복소수는 “수(number)”로서 인정받지 못했습니다.

허수가 정의되기 전 1세기에 고대 그리스의 발명가이자 수학자 “헤론(Ήρων)”이 음수의 제곱근에 대한 개념을 기록하면서 허수의 개념이 최초로 나타났고, 16세기에 와서야 허수가 정의되기 시작하였습니다.

[그림 1] 헤론

1572년에는 이탈리아의 수학자 “라파엘 봄벨리(Rafael Bombelli)”가 어떠한 2차방정식에선 음수의 제곱근을 취해야만 근을 구할 수 있었기 때문에 수를 확장하여 허수라는 새로운 종류의 수를 도입하였습니다.

[그림 2] 라파엘 봄벨리

예로 다음과 같이 2차방정식이 있을 때,

위 방정식은 2차방정식의 근의 공식을 이용하여 일반해를 구할 수 있습니다.

판별식 d 가 음수일 때

여기서 허수의 개념을 도입하지 않으면 음수가 아닌 수에 대해서만 실수의 제곱근이 있으므로 식 z 는 아무 의미도 없는 식이 됩니다. 즉, 식 z 는 허수가 정의되어야만 쓸 수 있는 식이 됩니다.

이와 비슷하게 이탈리아의 수학자 “니콜로 타르탈리아(Niccolo Tartaglia)”, 이탈리아의 의사이자 수학자 “지롤라모 카르다노(Girolamo Cardano)”와 같은 수학자들도 3차와, 4차, 다항방정식의 근에 대한 공식을 발견하면서 허수의 개념을 도입하였습니다.

[그림 3] 니콜로 타르탈리아

[그림 4] 지롤라모 카르다노

17세기에 “르네 데카르트(René Descartes)”가 “가상의 수”라는 뜻으로 허수라는 용어를 사용하기 시작했고,

[그림 5] 르네 데카르트

18세기에 스위스의 수학자 “레온하르트 오일러(Leonhard Euler)”는 허수단위의 기호로 i 를 도입했습니다(전자공학과 같은 분야에서는 전류를 i 로 표기하기 때문에 허수단위를 j 로 표기하는 경우도 있습니다).

[그림 6] 레온하르트 오일러

1799년엔 노르웨이의 수학자 “카스파르 베셀(Caspar Wessel)”이 “복소평면” 모델을 정의함으로서 복소수를 기하적인 표현으로 나타내었고, 19세기에 프랑스의 수학자 “아르강(Jean-Robert Argand)”이 베셀의 논문을 프랑스어로 번역하면서 부터 복소수는 수로 인정받기 시작했습니다. 그렇기에 복소평면을 “Argand 그림”이라고도 부르기도 합니다.

▶ 복소평면

복소평면은 간단히 복소수를 기하학적으로 표현하기 위해 개발된 모델입니다. 복소평면의 형태는 데카르트 좌표계와 같습니다. xy 좌표계에서 x 축을 실수축, y 축을 허수축이라 하고, 직교형식의 복소수

는 복소평면에서 다음과 같이 표현 됩니다.

[그림 7] 직교좌표의 복소평면

Re z 는 z 의 실수부 a 를, Im z 는 z 의 허수부 b 를 표현한 것 입니다. [그림 7]은 순서쌍 (a, b)의 직교형식을 직교좌표위의 한점으로 나타낸 것 인데, 해석기하학에서는 직교좌표(x, y)대신 극좌표(r, θ )를 이용하기도 합니다. 두 좌표형태를 다음과 같이 대응할 수 있습니다.